Graphs - 6

Covered in this section:

• Minimum Spanning Tree
• Minimum spanning forest

Minimum Spanning Tree

A spanning tree is a tree that contains N vertices and N-1 edges, where every vertex is connected to every other vertex. A minimum spanning tree is a spanning tree with the minimum sum of edge weights.

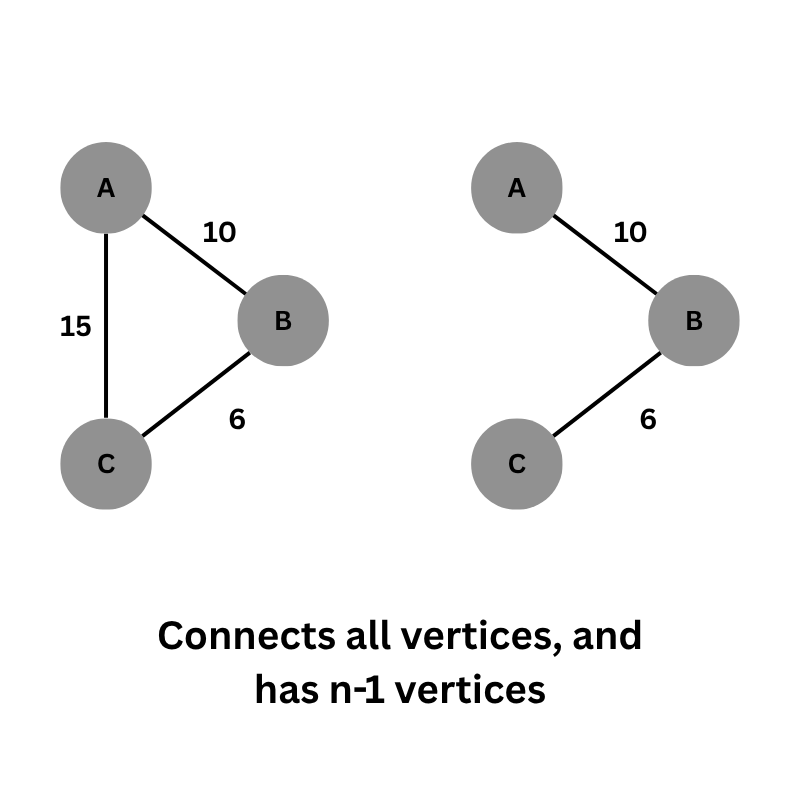
In the example above, we remove the edge between C and A, as its removal does not disconnect the graph—meaning all components remain connected. To find a Minimum Spanning Tree (MST), we typically use Kruskal's Algorithm or Prim's Algorithm.

Kruskal's Algorithm

Kruskal's MST algorithm is based on DSU, therefore DSU is a prerequisite for this learning this algorithm (graph - 4). The algorithm consists of three main steps:

1. Sort edges based on edge weight.
2. Check if both components are connect or not. We do this by comparing DSU elements
3. If they are not then connect them. After uniting them, do union operation on the two sets.

Prim's Algorithm

Prim's Algorithm is a greedy algorithm that finds the Minimum Spanning Tree (MST) of a connected, weighted graph. It starts from an arbitrary node and grows the MST by always choosing the edge with the smallest weight that connects a visited node to an unvisited node.

Steps:

1. Initialize a priority_queue (min-heap) to store edges in the form: (weight, to_node, from_node).
2. Push the starting edge: (0, 0, -1) into the priority queue.
   • 0 is the weight (no cost to start)
   • 0 is the starting node
   • -1 indicates no parent (root of the MST)
3. While the priority queue is not empty:
   • Pop the edge with the smallest weight.
   • If the destination node has already been visited, skip it.
   • Otherwise:
     • Mark the node as visited.
     • Add the edge to the MST.
     • Add the weight to the total MST cost.
     • Push all unvisited neighbors of the current node into the priority queue.

Concepts related to MST in programming contests

Maximum spanning tree

In Krushal's algorithm instead of sorting edges in ascending order, we sort in descinding order instead. In prim's algorithm instead of maintaining priority queue of ascending order, we maintain priority queue of descending order instead.

Minimum Spanning forest

For a disconnected graph (graph with multiple isolated parts), you can't have a single spanning tree. So, you create a spanning tree for each connected component, and together, these trees form a forest (a collection of trees).