DFS is a simple algorithm for traversing a graph. Everytime DFS reaches a branching node, it will visit one of the unvisited nodes and continue traversing until it reaches a dead end. Then it will backtrack to the last branching node and repeat the process. This is a recursive algorithm.
void dfs(graph, node, visited) {
if (visited[node]) return; // node is already visited
visited[node] = true; // mark node as visited
//Process node
for (neighbor in graph[node]) { // for each neighbor of the node
dfs(graph, neighbor, visited); // visit the neighbor
}
}
BFS is another algorithm for traversing a graph. It uses a queue to keep track of the nodes to visit. It starts from a node, marks it as visited, and adds all its neighbors to the queue. Then it processes the first node in the queue, marks it as visited, and adds all its neighbors to the queue. This process continues until the queue is empty.
void bfs(graph, start)
{
queue<int> q;
vector<bool> visited(graph.size(), false);
q.push(start); // add the starting node to the queue
visited[start] = true;
while (!q.empty()) {
int node = q.front(); // get the first node in the queue
q.pop(); // remove the first node from the queue
//Process node
for (neighbor in graph[node]) { // for each neighbor of the node
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor); // add it to the queue
}
}
}
}
BFS and DFS both can be used to find number of connected components of the graph and count size of each component. (a.k.a Flood Fill algorithm)
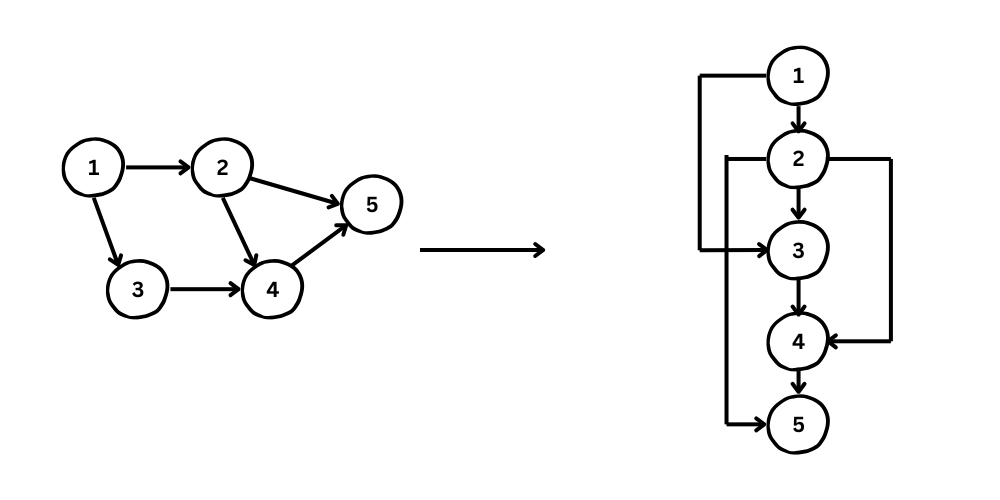
Topological sort is order is used to process nodes in a Directed Acyclic Graph. It is a linear ordering of vertices such that for every directed edge u => v, vertex u comes before v in the ordering. Topological sort can be done using DFS or Kahn's algorithm.
In this method, we will use a stack to keep track of the nodes in the topological order. We will start from a node, mark it as visited, and add it to the stack. Then we will visit all its neighbors recursively. After visiting all the neighbors, we will add the node to the stack. Finally, we will pop all the nodes from the stack to get the topological order.
void topodfs(graph, node, visited, stack) {
if (visited[node]) return;
visited[node] = true; // mark as visited
for (auto neighbors : graph[node]) {
topodfs(graph, neighbor, visited, stack); // visit the neighbor
}
stack.push(node); // add the node to the stack
}
Kahn's algorithm utlizes a modified version of BFS to find the topological order of a graph. It uses a queue to keep track of the nodes with no incoming edges (i.e. indegree 0). It starts from these nodes, adds them to the topological order, and removes their outgoing edges. If a node's indegree becomes 0, it is added to the queue. This process continues until all nodes are processed.
// Kahn's algorithm for topological sort
priority_queue<int, greater<int>> q; // min priority queue
vector<int> indegree(graph.size(), 0);
vector<int> topo_order;
for (int i = 0; i < graph.size(); i++) {
for (auto neighbor : graph[i]) {
indegree[neighbor]++; // calculate indegree of each node
}
}
for (int i = 0; i < graph.size(); i++) {
if (indegree[i] == 0) {
q.push(i); // add nodes with indegree 0 to the queue
}
}
while (!q.empty()) {
int node = q.top(); // get the first node in the queue
q.pop(); // remove the first node from the queue
topo_order.push_back(node); // add the node to the topological order
for (auto neighbor : graph[node]) {
indegree[neighbor]--; // remove the edge from the node
if (indegree[neighbor] == 0) {
q.push(neighbor); // if indegree becomes 0, add it to the queue
}
}
}
Note that Kahn's algorithm is more efficient than DFS based topological sort in terms of time complexity.
Before we apply topological sort, we need to check if the graph is a DAG (Directed Acyclic Graph). If the graph has a cycle, then topological sort is not possible and will go into infinite loop. We can use DFS or Kahn's algorithm to check for cycles.
We keeo track of the nodes in the current path using a visited array. If we encounter a node that is already in the current path, then we have found a cycle. We can use a recursive function to traverse the graph and check for cycles. Only visited array will not suffice here. This YT video explains the concept in detail.
Cycle detection using BFS is also possible => use Kahn's algorithm to find topological order. If the topological order does not contain all the nodes, then there is a cycle in the graph. This is because Kahn's algorithm only works for DAGs and will not be able to process all nodes if there is a cycle.