Dynamic Programming - 3

Covered in this section:

• Problems on 2-D DP

Maximal Square (Leetcode)

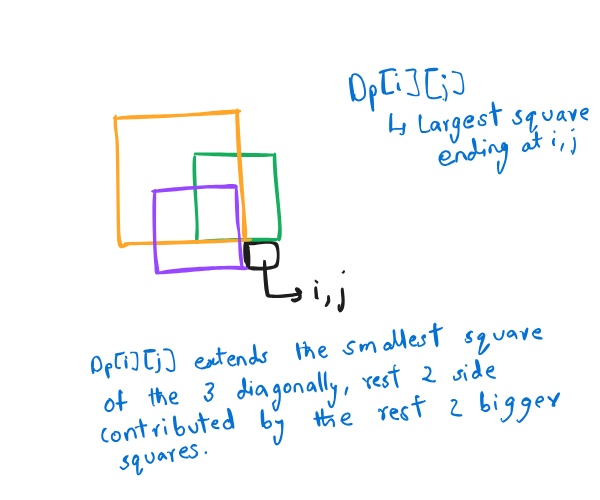
This problem asks us to find the largest square containing only 1s in a binary matrix. A brute-force approach would involve checking every possible square, leading to high time complexity. Instead, we use dynamic programming where dp[i][j] represents the size of the largest square ending at cell (i, j). The image above explains the intuition of the solution. Here is the pseudo-code that solves this problem.

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < m; j++) {
            if(matrix[i][j] == '1') {
                if(i == 0 || j == 0) {
                    dp[i][j] = 1;
                } else {
                    dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
                }
                ans = max(ans, dp[i][j]);
            } else {
                dp[i][j] = 0;
            }
        }
    }